Category Theory Note 2 Newbie Composition and Morphisms
Isomorphism or invertible map will be discussed in this chapter.
Isomorphism as Invertible Map
The crucial part of such map property is that an inverse map exists that $f: A \longrightarrow B$ has a $g$ inverse that satisfies $g \circ f \equiv 1_A$ and $f \circ g \equiv 1_B$.
A similarity between two collections can be given by choosing a map, which maps each element from the first one to the second one.
Thus isomorphism is also called invertible map. $A,B$ two objects are said to be isomorphic if an isomorphism $f:A\longrightarrow B$ exists. Properties:
- Reflexive: $A$ is isomorphic to $A$.
- Symmetric: If $A$ is isomorphic to $B$, $B$ is isomorphic to $A$.
- Transitive: If $A$ is isomorphic to $B$, $B$ is isomorphic to $C$, $A$ is isomorphic to $C$.
Thus it is obvious that $1_A$ is an isomorphism, if $f:A\longrightarrow B$ is an isomorphism, $g$ as inverse of $f$ is also an isomorphism.
It is also obvious that the inverse (if exists) of any map $f$ is unique, which means only one $g$ be $f-$inv or $f^{-1}$.
Two simple problems may occur, one is “determination“ or “extension“
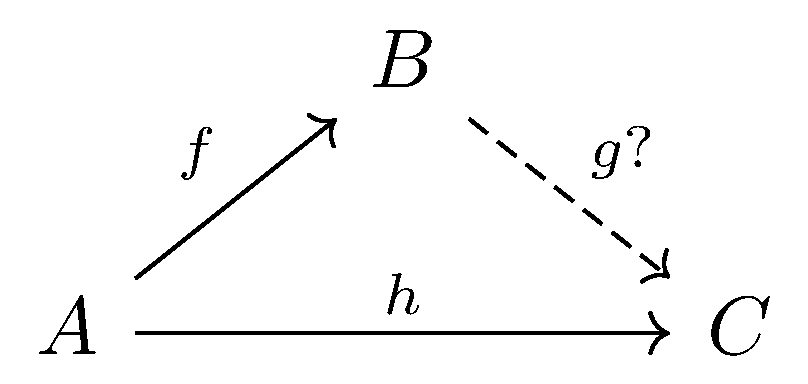
and the other one is “choice“ or “lifting“
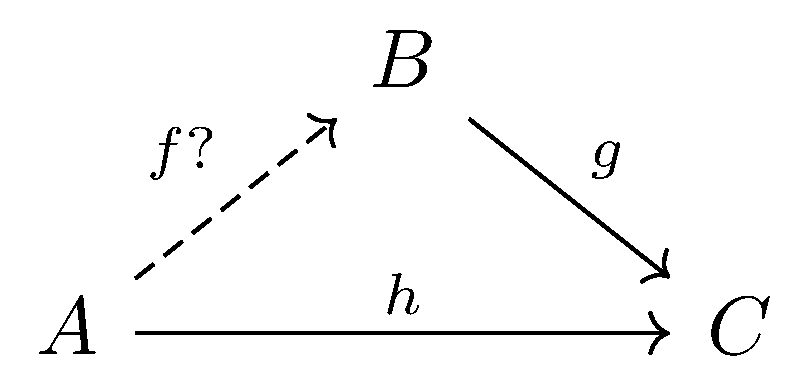
Examples
What if we have “determination“ problem with $B = \boldsymbol{1}$, which makes
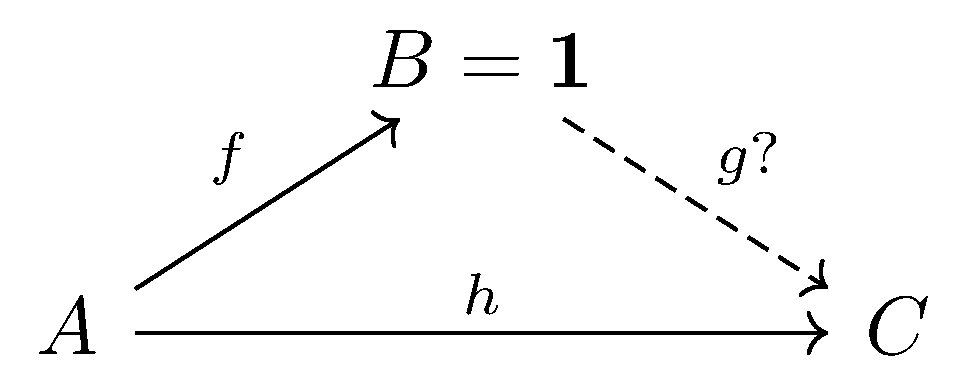
It is easy to see that $g$ is a point to $C$, which means $g:\boldsymbol{1}\longrightarrow C$. Thus $h(x)$ for $x \in A$ have $h(x) = (g \circ f)(x) = g(b)$ for $b \in B \equiv \boldsymbol{1}$.
In this way, $h$ is a constant because $\forall x \in A$, $h$ maps them to a single value $g(b)$ on $C$.
Another example here is on “choice“ problem with $A = C$, which makes
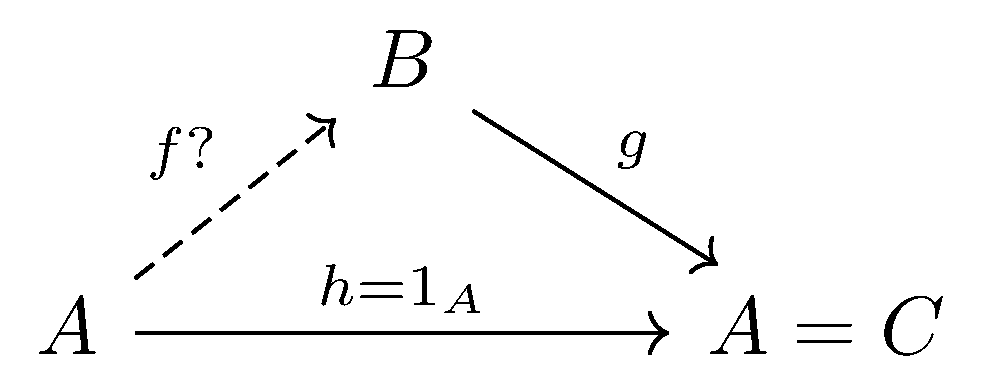
To make things easier, we give a small example
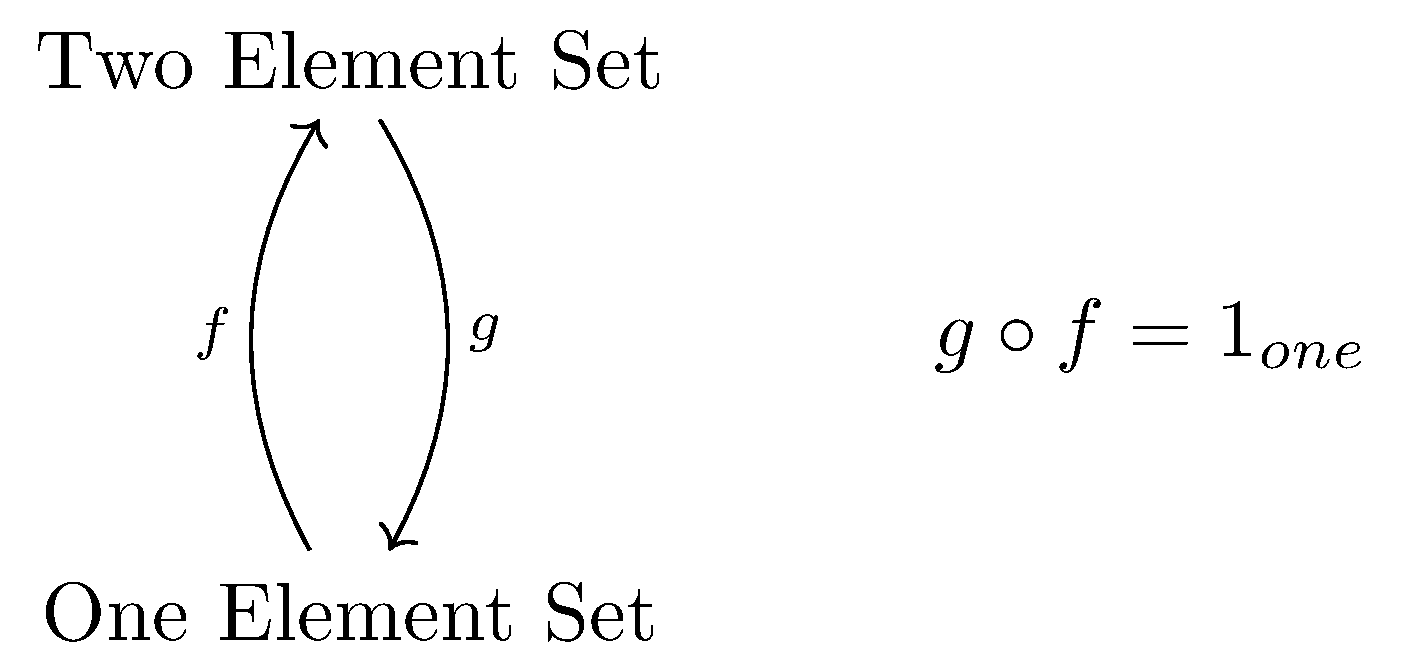
It is not hard to see that $g$ is constant and $f$ has two choices. The only way for $f$ existence is that $|B| \ge |A|$ and every element in $C$ is mapped.
Retraction, Section
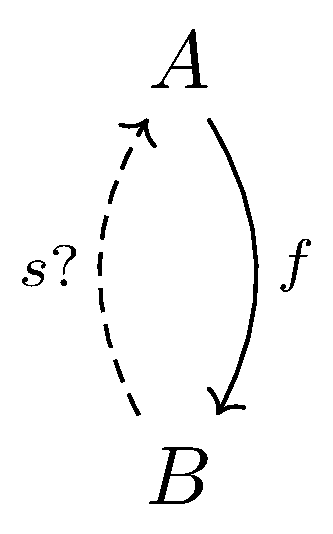
Retraction can be defined if $f:A \longrightarrow B$, a retraction for $f$ is a map $r :B \longrightarrow A$ for which $r \circ f = 1_A$. The determination problem can be simplified in a way shown in following pictures.
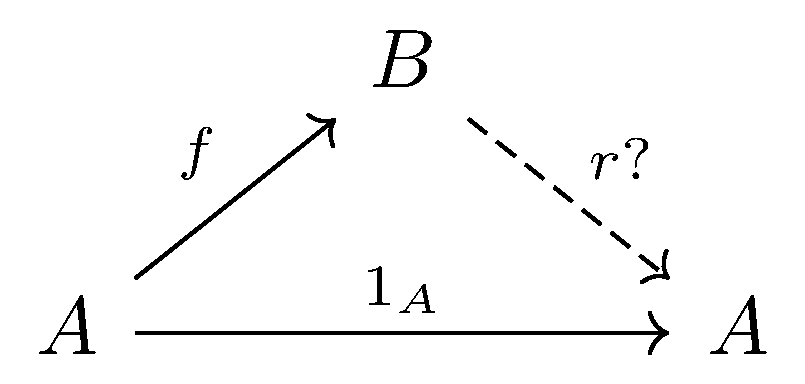
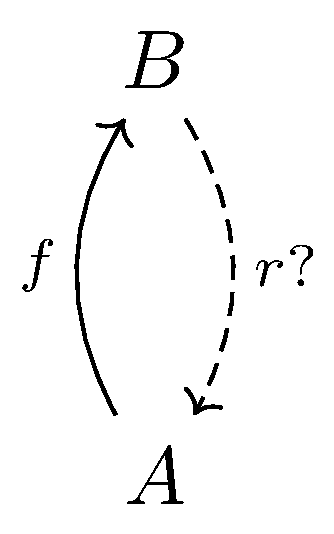
Section can be defined if $f : A \longrightarrow B$, a section for $f$ is a map $s: B\longrightarrow A$ for which $f \circ s = 1_B$. The choice problem can be simplified in a way shown in following pictures.
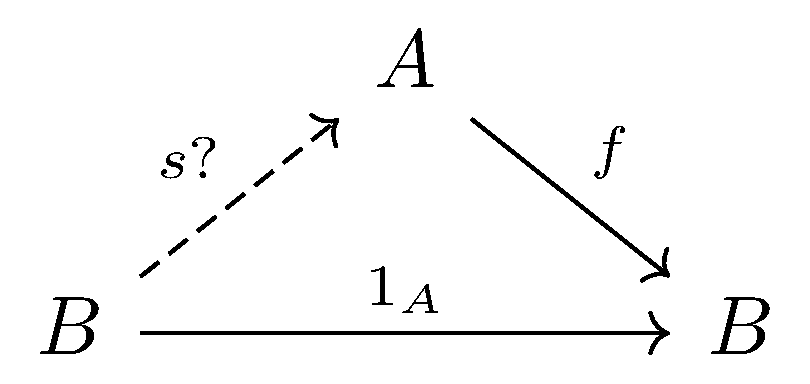
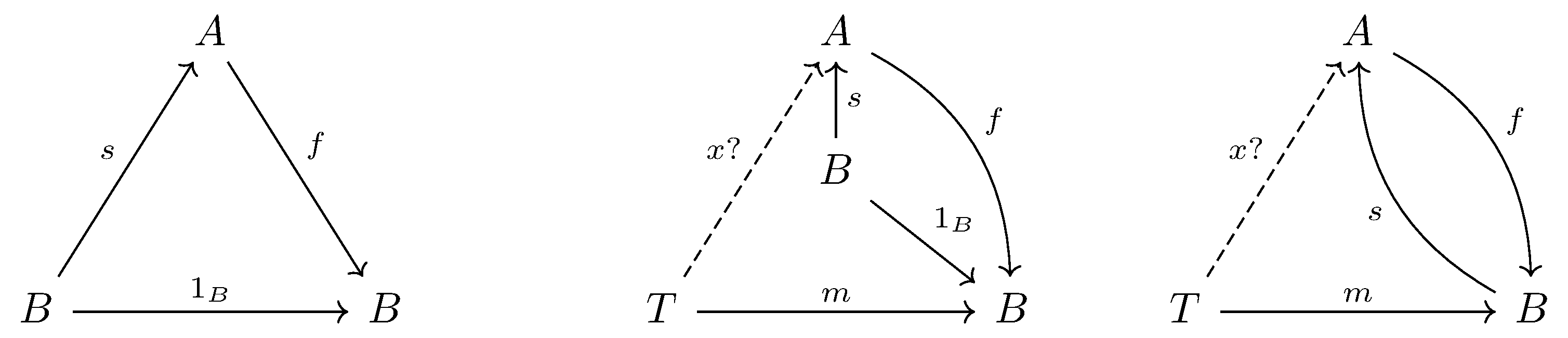
It is not hard to see that, if $f:A\longrightarrow B$ has a section $s:B\longrightarrow A$, then $\forall T$ and $\forall m:T\longrightarrow B, \exists x:T\longrightarrow X$ that $f \circ x = m$.
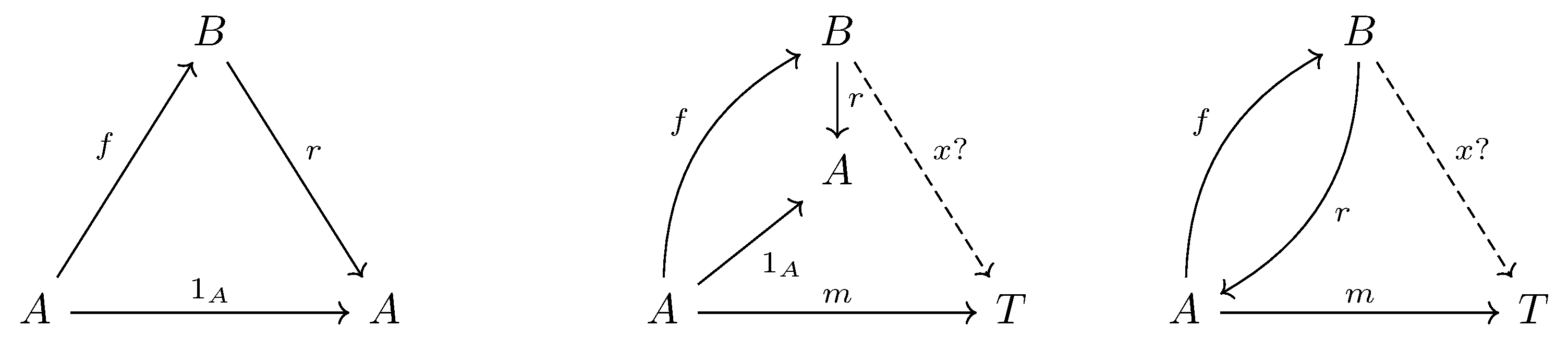
The dual version is: If $f:A\longrightarrow B$ has a retraction $r:B\longrightarrow A$, then $\forall T, \forall m: A\longrightarrow T, \exists x: B\longrightarrow T$ that $x \circ f = m$.
Epimorphism, Monomorphism, Idempotent
Suppose $f:A\longrightarrow B$ has a retraction, then $\forall T, \forall x_1, x_2:T\longrightarrow A$, if $f \circ x_1 = f\circ x_2$, then $x_1 = x_2$.
A map $f$ satisfying this conclusion is said to be injective for maps from $T$. If $\forall T$ is satisfied, then $f$ is injective, or is a monomorphism.
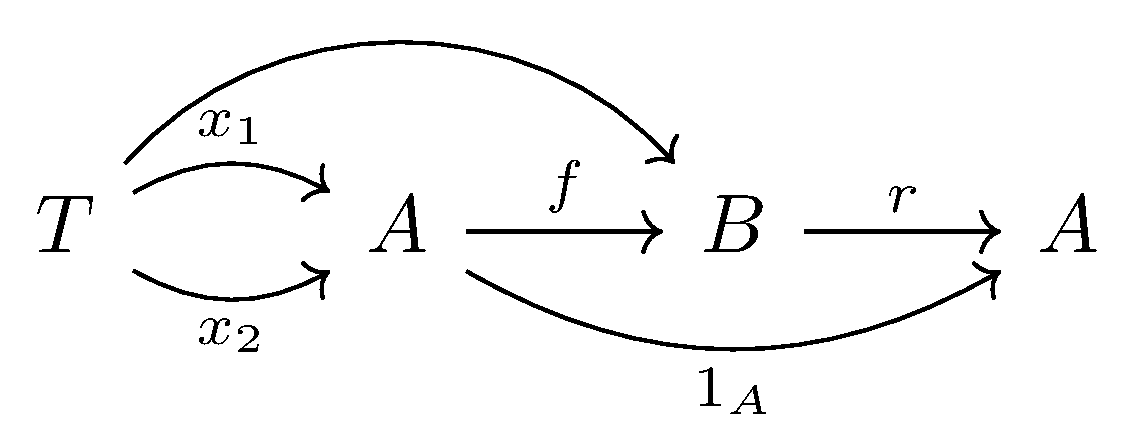
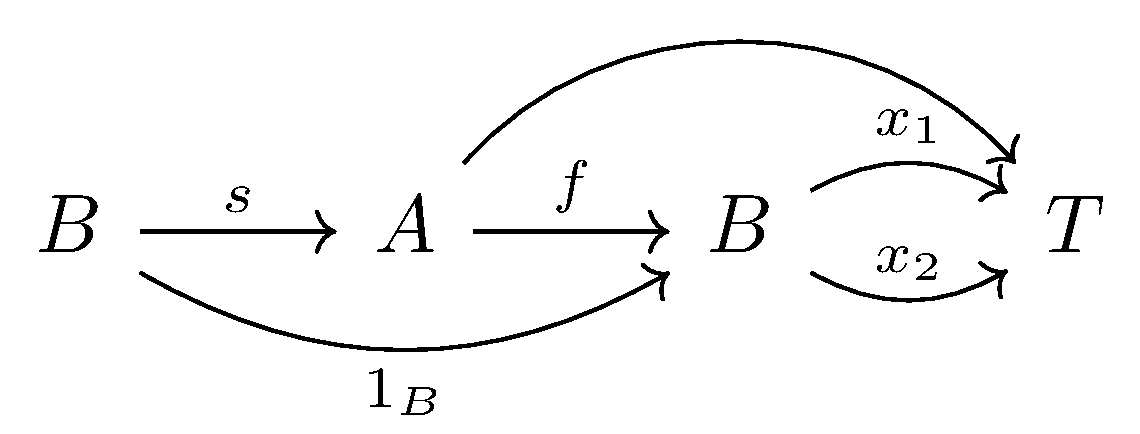
The dual version is that $f :A\longrightarrow B$ has a section, then $\forall T, \forall x_1, x_2:B \longrightarrow T$, if $x_1 \circ f = x_2 \circ f$, then $x_1 = x_2$.
A map $f$ with cancellation property ($x_1 \circ f = x_2 \circ f$ then $x_1 = x_2$) for any $T$ is called epimorphism.
Both epimorphism and monomorphism are cancellation properties.
An endomap $e$ is called idempotent if $e \circ e = e$.
If $f: A\longrightarrow B$ has both a retraction $r$ and a section $s$, then $r = s$.
Isomorphism, Automorphism
We can rephrase isomorphism with retraction and section:
A map $f$ is called an isomorphism if $\exists f^{-1}$ which is both a retraction and a section for $f$ that $f \circ f^{-1} = 1_B$ and $f^{-1} \circ f = 1_A$.
A map, which is an isomorphism and an endomap at a same time, is an automorphism.
In general, if any isomorphism exists for $A\longrightarrow B$, there are the same number of them as there are automorphism of $A$, and this can be proved without counting.
Let $Aut(A)$ be the set of all automorphisms of $A$ and $Isom(A,B)$ be the set of all isomorphisms of $A\longrightarrow B$. We just need to construct isomorphism between those two sets.
If $f : A\longrightarrow B$ is an isomorphism, then $F : Aut(A)\longrightarrow Isom(A,B)$ can be constructed by $F(\alpha) = f\circ \alpha$ for any automorphism $\alpha$ on $A$.
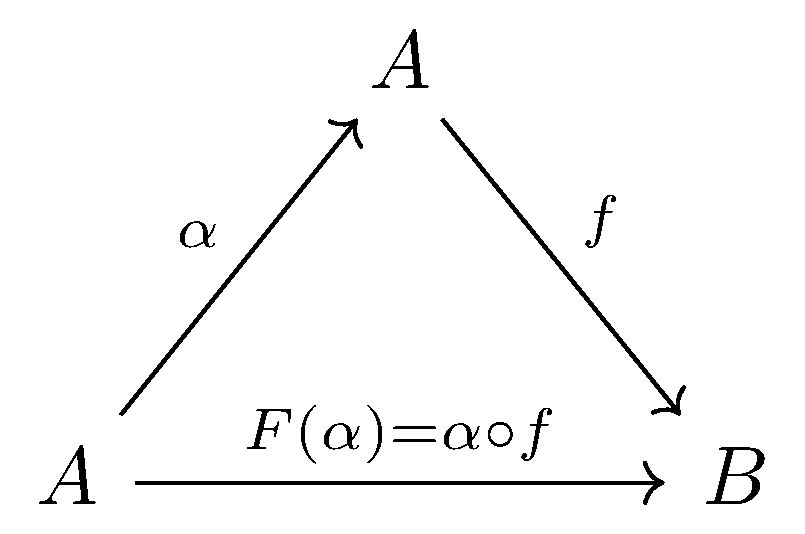
$F(\alpha) \in Isom(A,B)$, and we want to show $F$ itself is an isomorphism, by constructing $S = F^{-1}: Isom(A,B)\longrightarrow Aut(A)$.
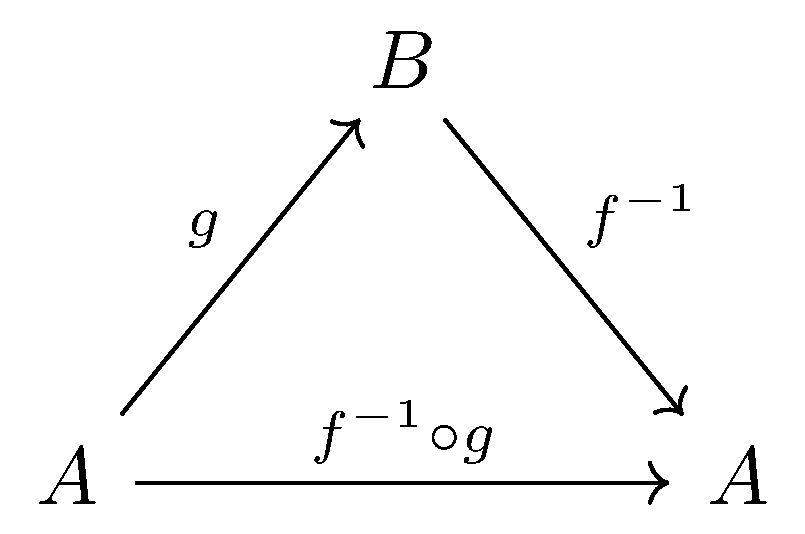
Thus, $S(g) = f^{-1} \circ g$.
$$
\begin{aligned}
(F \circ S)(g) &= F(S(g))= F(f^{-1}\circ g) = f \circ (f^{-1}\circ g) = g\newline
(S \circ F)(\alpha) &= S(F(\alpha)) =S (f\circ \alpha) = f^{-1} \circ(f\circ \alpha) = \alpha
\end{aligned}
$$
We can see that $F\circ S = 1_{Isom(A,B)}$ and $S\circ F = 1_{Aut(A)}$.
Automorphism, or Permutation
An automorphism in category of sets is traditionally called a permutation, suggesting that it shifts elements of its sets around in a specified way.
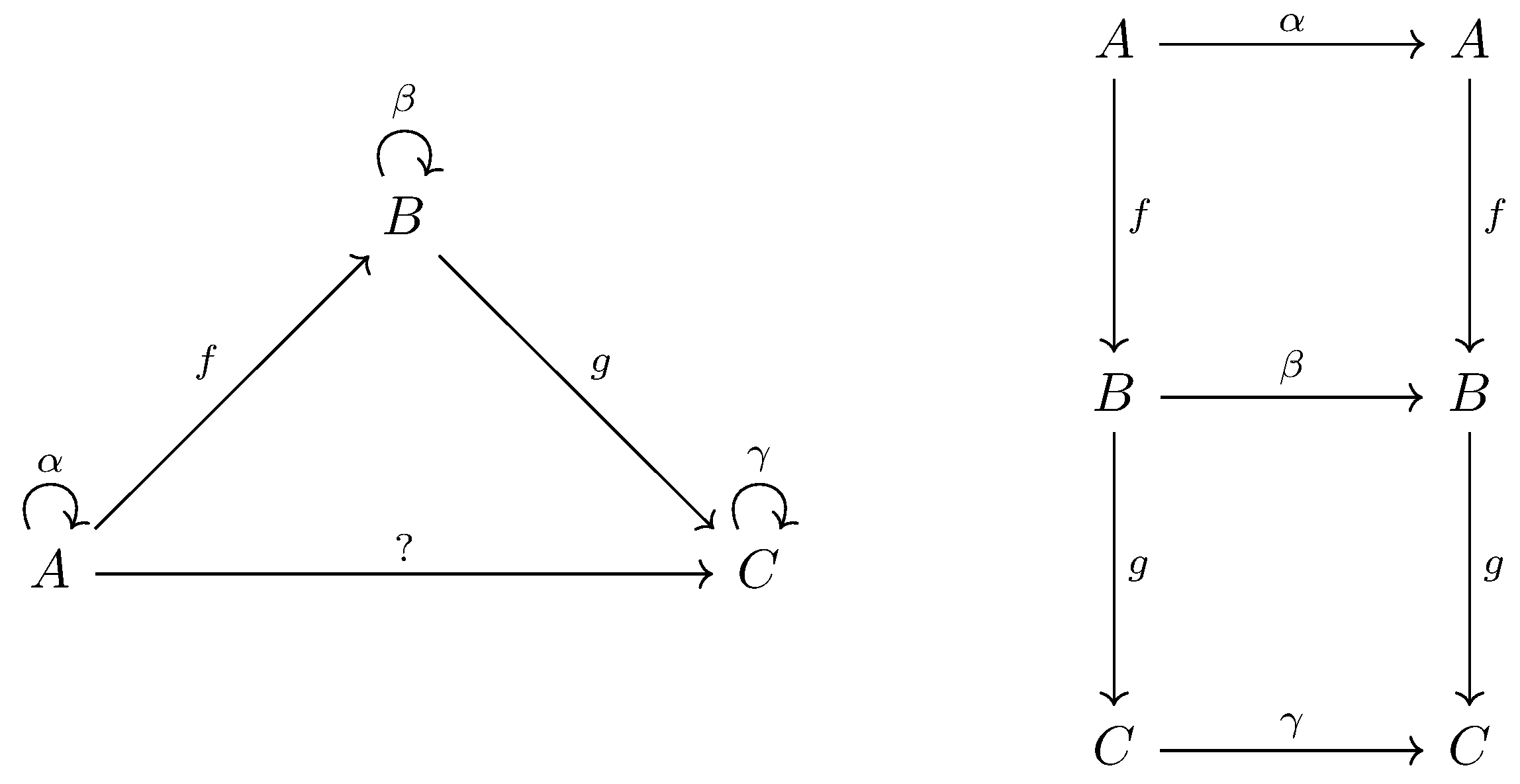
A category of permutation has an object defined with a set $A$ and an automorphism $\alpha$. Thus an object is defined as $A^{\Large\circlearrowright_\alpha}$.
A map from $A^{\Large\circlearrowright_\alpha}$ to $B^{\Large\circlearrowright_\beta}$ is a map of $f : A\longrightarrow B$ which preserve the automorphisms $\alpha$ and $\beta$ in a sense that $f \circ \alpha = \beta\circ f$.
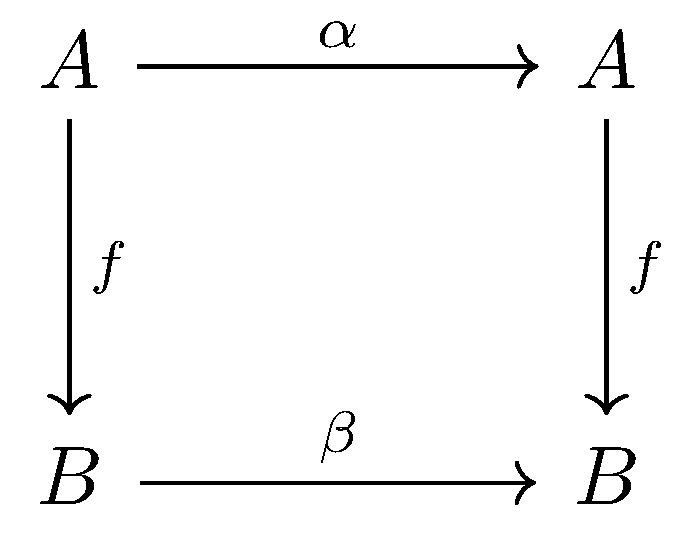
If $g$ is a map from $B^{\Large\circlearrowright_\beta}$ to $C^{\Large\circlearrowright_\gamma}$, and we want to compose $f$ and $g$, the natural thing is to compose them as $A \overset{f}{\longrightarrow} B \overset{g}{\longrightarrow} C$.
The verification is shown in the following commutative diagram, which indicates $g \circ f \circ \alpha = g \circ \beta\circ f = \gamma \circ g \circ f$.