Graduate Cryptography Note 3
All info comes from David Wu’s Lecture and Boneh-Shoup Book.
This note will be focusing on methods of constructing block ciphers, with examples like DES and AES, and message integrity.
Typically we rely on iteration to construct block ciphers, where key expansion relies on a PRG.
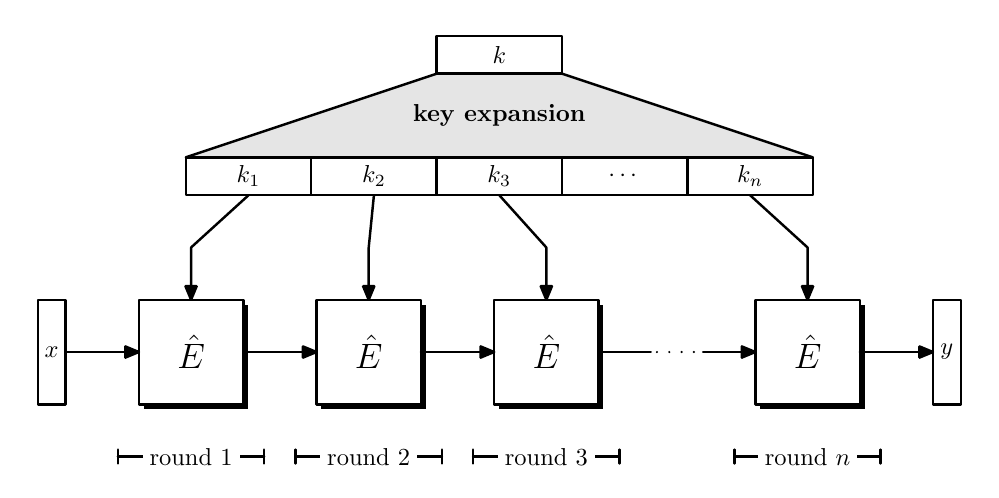
Since $\hat{E}(k,x) \to y$, which is a round function, we have $|x| = |y|$, where $n$ times applied $\hat{E}$ constructed a PRF or PRP.
DES (Data Encryption Standard with Feistel Structure)
DES relies on Feistel design, where $|L_0| = |R_0|$. We have $L_1 \gets F_k(R_0)$ and $R_1 \gets L_0 \oplus L_1$.
Even if $F(k,\cdot):\lbrace 0,1\rbrace^n \times \lbrace 0,1\rbrace^k \to \lbrace 0,1\rbrace^n$ is non-invertible, Feistel round function $\Psi_F:\lbrace 0,1\rbrace^{2n} \to \lbrace 0,1\rbrace^{2n}$ is still invertible, noticing $\lbrack L_0,R_0\rbrack \mapsto \lbrack R_0, L_0 \oplus F(k, R_0)\rbrack \equiv \lbrack L_1, R_1\rbrack$.
If we have $R_0$ or $L_1$, then we can construct $L_0 \gets R_1 \oplus L_1$ (on $R_0$ we have $L_1 \gets F_k(R_0)$).
Luby-Rackoff Theorem
If $F$ is a secure PRF, then 3-round Feistel with independent $k$ yields a secure PRP.
This shows that Feistel network is a good heuristic for block cipher design, so long as we have $F$ as PRF.
The practical usage here uses 16 round Feistel function since we hope $F$ scramble enough times will confuse all the adversary.
Feistel Round Function
The block size of DES is 64 bit and key size is 56 bit. For each S-Box $F$, the key size is 48 bit.
DES generate each 48-bit key from the 56-bit key, a simple way is that each 48-bit key is a subset of the original 56-bit key.
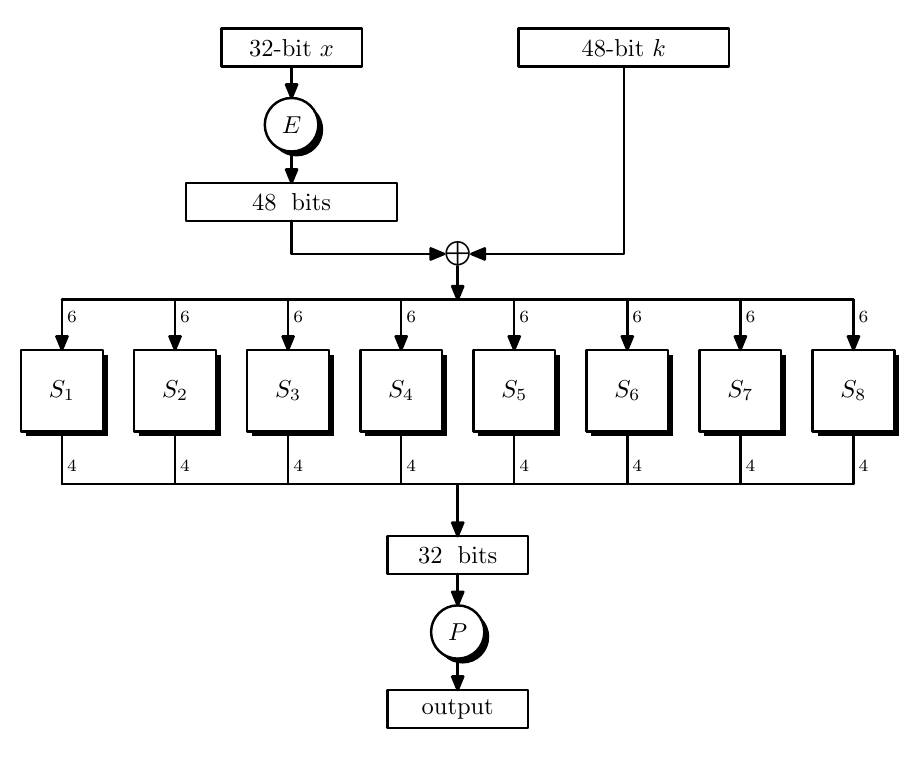
- $E$ expands 32-bit input into 48-bit output by rearranging and replicating these input bits.
- $P$ is a mixing permutation, maps 32-bit input to 32-bit output by rearranging.
- $S_i$ is S-Box (substitution box), maps 6-bit to 4-bit by some truth table. They are highly non-linear functions, which is the source of non-linearity in the design.
AES (Even-Mansour)
Even-Mansour construction follows $y \gets k_2 \oplus \pi (x \oplus k_1)$, where $\pi$ is a permutation.
The inversion from $y$ to $x$ can be constructed by $\pi^{-1}$ where $x \gets k_1 \oplus \pi^{-1}(k_2 \oplus y)$.
Even-Mansour Theorem
If $\pi$ is modeled as a random permutation, then Even-Mansour cipher is a secure PRP.
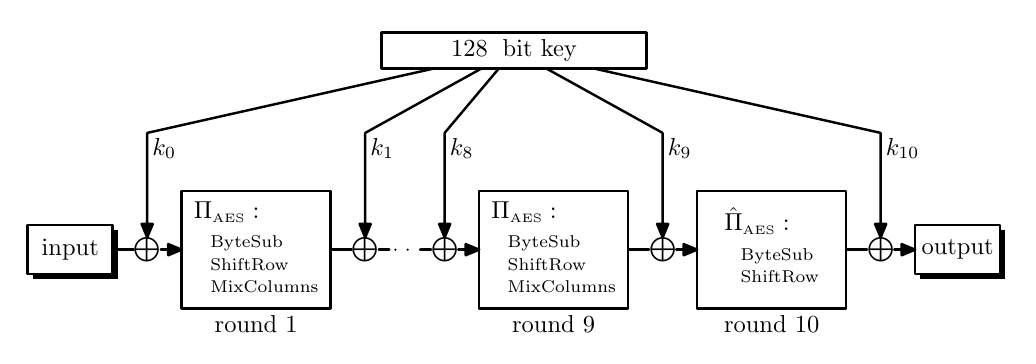
Details about SubBytes, ShiftRows, MixColumns can go to previous note.
Message Integrity and Message Authentic Code (MAC)
Message Integrity is needed when adversary can temper with message. A “tag”, or a signature, is appended to a message to prove integrity.
The signature should be computed with a keyed-function, or it can be forged by any other adversary.
MAC
A MAC with key-space $\mathcal{K}$, message space $\mathcal{M}$ and tag space $\mathcal{T}$ is a tuple of algorithms $\pi_{MAC} = (\text{Sign, Verify}): \begin{cases}\text{Sign}&\mathcal{K\times M\to T}\newline \text{Verify} &\mathcal{K\times M\times T}\to\lbrace 0,1\rbrace \end{cases}$.
$(\text{Sign, Verify})$ must be efficiently computable. The correctness of such algorithm is guaranteed by $\forall k \in \mathcal{K}, \forall m \in \mathcal{M}, \Pr\lbrack \text{Verify}(k,m,\text{Sign}(k,m)) = 1\rbrack = 1$.
Intuitively an adversary cannot compute a signature without any knowledge of the key. It should also not be able to know anything about key on existing message or signature.
A MAC satisfies existential unforgeability against chosen message attack if $\forall \mathcal{A}$, $\text{MACAdv}\lbrack\mathcal{A},\pi_{MAC}\rbrack = \Pr\lbrack W=1\rbrack = \text{negl}(\lambda)$, where $W$ is the output of the security game.
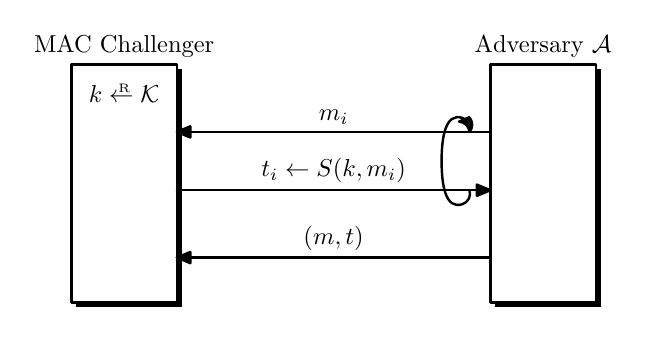
$W = 1 \iff \text{Verify}(k, m^\ast, t^\ast) = 1$ and $(m^\ast,t^\ast)\notin\lbrace (m_1,t_1),\dots,(m_q, t_q)\rbrace$, where $q$ donates the query number.
MAC from PRF
Let $F :\mathcal{K\times M\to T}$ be a secure PRF, then we have $\begin{cases}\text{Sign}(k,m)&\text{output }t\leftarrow F(k,m)\newline\text{Verify}(k,m,t)&\text{output } 1\text{ if }t = F(k,m)\text{ and }0\text{ otherwise}\end{cases}$ to be $\pi_{MAC}$ over $(\mathcal{K,M,T})$.
Theorem: If $F$ is a secure PRF with a sufficient large range, $\pi_{MAC}$ defined above is a secure MAC. For every efficient MAC adversary $\mathcal{A}$, there exists an efficient PRF adversary $\mathcal{B}$ such that
$$
\text{MACAdv}\lbrack \mathcal{A},\pi_{MAC}\rbrack \le \text{PRFAdv}\lbrack \mathcal{B},F\rbrack + \dfrac{1}{|\mathcal{T}|}
$$
Proof intuitive goes like:
- PRF is computationally indistinguishable from the truly random function.
- If we replace PRF with truly random function from $\text{Func}\lbrack\mathcal{M,T}\rbrack$, adversary wins the MAC game with only $\dfrac{1}{|\mathcal{T}|}$ probability.
If we want to sign a longer message, we can look into two types of constructions:
- Constructing a large-domain PRF from a small-domain PRF
- Hash-based construction
CBC-MAC
CBC without an IV can build a MAC and we often call this raw-CBC.
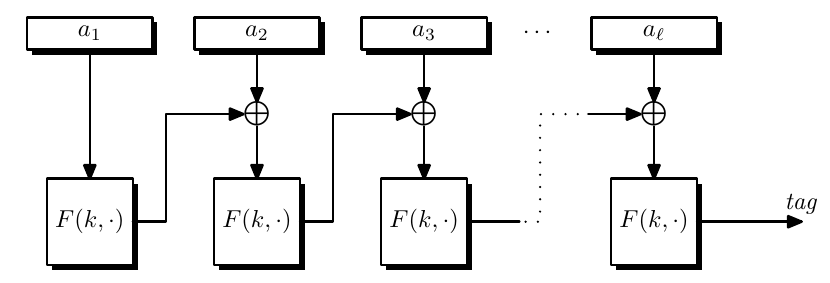
But raw-CBC is not security for shared-prefix messages, namely it is secure for prefix-free messages.
The attack can be formulated:
- We query for MAC on an arbitrary block $x$ and get a $t = F(k, x)$.
- We then query MAC on message $(x, x\oplus t)$ and get $t$ again.
So adversary succeed with probability 1.
ECBC
raw-CBC is used to build a MAC on fixed length messages, we can construct MAC for variable-length messages by Encrypted-CBC (ECBC).
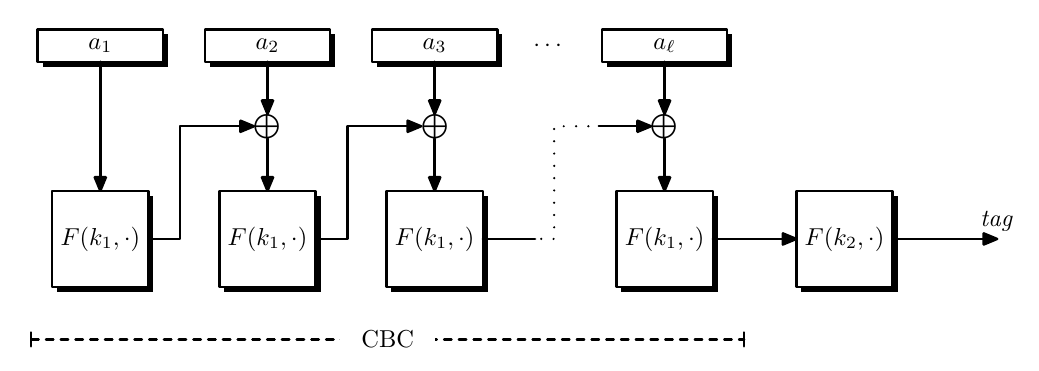
The current CBC constructed MAC must use a message length of multiple of block size. We must introduce padding function. It must be injective or different message may end up with same MAC.
A standard padding is $\texttt{0b1000…}$ since it will guarantee no collision and easy to be implemented.
ECBC limitations are
- Always need two keys for PRF
- Messages need padding
We can try raw CBC-MAC message with prefix-free messages like prepend message length to the message.
But it is problematic if we do know the message length like streaming.
CMAC
Or it can secretly do a random shift to the last block of the message $(x_1,x_2,\dots,x_n)\mapsto (x_1,x_2,\dots,x_n\oplus k)$ where $k \overset{R}{\leftarrow}\mathcal{X}$, this is called cipher-based MAC (CMAC).
Adversary wins the game with advantage $\dfrac{1}{|\mathcal{X}|}$ if he can guess $k$.
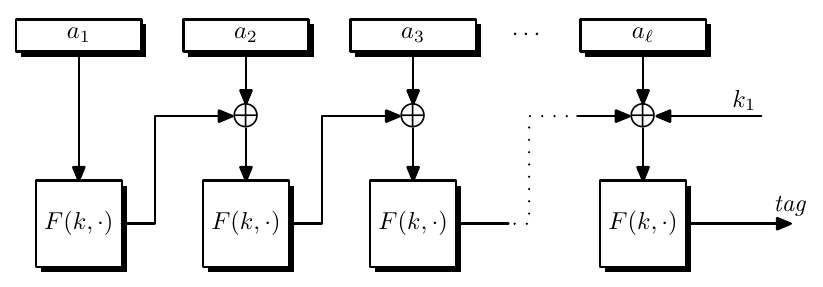
The key for CMAC is $(k, k_1, k_2)$ where $k_1$ is for unpadded and $k_2$ is for padded.
Cascade Design
Nested MAC construction is constructed as follows and the total key needed are $(k, k_2)$.
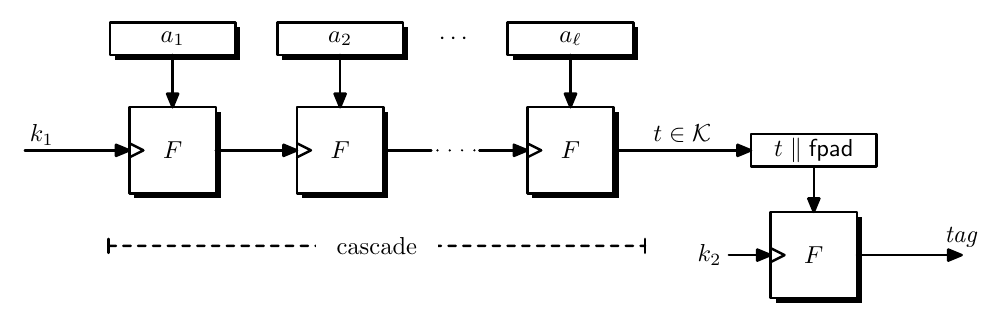
If the $\mathcal{K}$ is smaller than $\mathcal{X}$, then we need to use pad, the padding is just a hard-coded constant, which can be string of $0$s.
Theorem: Let $F:\mathcal{K\times X\to X}$ in CMAC and $F:\mathcal{K\times X \to K}$, then for all MAC adversaries $\mathcal{A}$, exists a PRF adversary $\mathcal{B}$ where
$$
\begin{aligned}
\text{MACAdv}\lbrack\mathcal{A},\pi_{ECBC}\rbrack &\le 2\cdot \text{PRFAdv}\lbrack \mathcal{B},F\rbrack + \dfrac{Q^2(l+1)^2}{|\mathcal{X}|}\newline
\text{MACAdv}\lbrack\mathcal{A},\pi_{NMAC}\rbrack &\le (Q(l+1) + 1)\cdot \text{PRFAdv}\lbrack \mathcal{B},F\rbrack + \dfrac{Q^2}{2|\mathcal{K}|}
\end{aligned}
$$
So first we can try to prove that for every prefix-free PRF adversary $\mathcal{A}$ attacks $F_{CBC}$ and issues at most $Q$ queries, exists PRF adversary $\mathcal{B}$ that attacks $F$ such that
$$
\text{PRF}^{\text{pf}}\text{adv}\lbrack\mathcal{A},F_{CBC}\rbrack \le \text{PRFAdv}\lbrack\mathcal{B},F\rbrack + \dfrac{(Ql)^2}{2|\mathcal{X}|}
$$
We present adversary’s queries in a rooted tree, where edges are labeled with message blocks $a_i$, defines a path in a tree from root: $root \overset{a_1}{\rightarrow} p_1 \cdots \overset{a_v}{\rightarrow} p_v$ ($m = (a_1,\dots,a_v) \in \mathcal{X}^v, 1 \le v\le l$).We associate a value $\gamma_p\in\mathcal{X}$ to the computed value in CBC query tree. Define $\gamma_{root} = 0^n$ and $p\overset{a}{\rightarrow}q$ to be $\gamma_q = F(k,a \oplus \gamma_{p})$.
We use PRF in the CBC mode.
Replace $F(k,\cdot)$ with some $f \overset{R}{\leftarrow}\text{Funs}\lbrack\mathcal{X,X}\rbrack$.
Make the $f$ a “faithful gnome”, which means the challenger prepares random variables $\beta_i\overset{R}{\leftarrow}\mathcal{X}$ where $i = 1,\dots,B = (Ql)$.
The challenger must satisfy
- $\gamma_q\leftarrow \beta_i$
- If $\exists$ another edge $p’\overset{a’}{\rightarrow} q’$ with $\gamma_{p’}\oplus a’ = \gamma_p \oplus a$ then $\gamma_q \leftarrow \gamma_{q’}$.
Make the Challenger forgetful, which means we only follow $\gamma_q \leftarrow \beta_i$.
If we want to analyze the change, we can suppose for distant pair of edges $p \overset{a}{\rightarrow} q$ and $p’ \overset{a’}{\rightarrow} q’$, and we have $\gamma_{p’}\oplus a’ = \gamma_p \oplus a$.
There is no way $p = p’$ since edges are distant, we must have $a \ne a’$ or $\gamma_{p’}\oplus a’ = \gamma_p \oplus a$ will not hold.
Since $\mathcal{A}$ never know anything about $\gamma_{p’}$ and $\gamma_{p}$, then $\gamma_p \oplus \gamma_{p’}$ is uniformly distributed over $\mathcal{X}$. By $a’ \oplus a = \gamma_p \oplus \gamma_{p’}$, we know that $\gamma_p \oplus \gamma_{p’}$ is independent of $a \oplus a’$.
Thus $|\Pr\lbrack W_0\rbrack - \Pr\lbrack W_1\rbrack | = \text{PRFAdv}\lbrack\mathcal{B},F\rbrack$, $\Pr\lbrack W_2 \rbrack = \Pr\lbrack W_1 \rbrack$, $|\Pr\lbrack W_2\rbrack - \Pr\lbrack W_3\rbrack |\le \dfrac{(Ql)^2}{2|\mathcal{X}|}$.
Also we need to know for every PRF adversary $\mathcal{A}$ that attacks $F^\ast$, the cascade of $F$, at most $Q$ queries. There exists PRF adversary $\mathcal{B}$ that attacks $F$ where $\mathcal{B}$ is a wrapper around $\mathcal{A}$ such that
$$
\text{PRF}^\text{pf}\text{adv}\lbrack\mathcal{A},F^\ast\rbrack \le Ql\cdot \text{PRFadv}\lbrack \mathcal{B},F\rbrack
$$
We can build a tree construction, which combines hybrid argument (which is described in 4.6 Boneh Book) in cascaded PRFs. Also it is a $Q$ queries in parallel, which adds a $Q$ coefficient.
Let $PF$ be an extendable and prefix-free secure PRF defined over $(\mathcal{K_1, X^{\le l}, Y})$, $F$ be a secure PRF defined over $(\mathcal{K_2,Y,T})$. Then $EF$ is a secure PRF defined over $(\mathcal{K_1 \times K_2, X^{\le l},T})$.
Forall PRF adversary $\mathcal{A}$ that attacks EF at most $Q$ queries exists PRF adversary $\mathcal{B}_1$ attacks $F$ and $\mathcal{B}_2$ prefix-free PRF adversary attacks $PF$, where $\mathcal{B_1,B_2}$ are wrappers around $\mathcal{A}$, such that
$$
\text{PRFadv}\lbrack \mathcal{A},EF\rbrack \le \text{PRFadv}\lbrack\mathcal{B}_1,F\rbrack + \text{PRF}^\text{pf}\text{adv}\lbrack\mathcal{B_2},PF\rbrack + \dfrac{Q^2}{2|\mathcal{Y}|}
$$
In this way MAC adv are proved trivially by the last theorem and the previous two theorems.